|
|||
|
Accueil Catalogue Atelier - Vidéos 
Commander... Nous écrire... Google Earth (Localisez Fusion d'Argile avec) Stages Formations Emploi Partenaires, liens... Conditions de vente    |
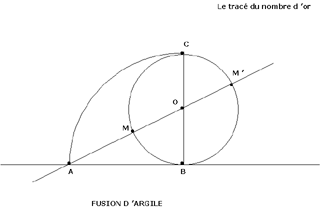
Le tracé du Nombre d'Or...
|
Face à la conjoncture, la poterie artisanale Fusion d'Argile a pris l'option de cesser ses activités. L'atelier et la boutique sont donc définitivement fermés, et ce site n'est et ne sera plus maintenu !(octobre 2009). Nous tenons simplement ici à remercier tous nos clients quant à leur attention, enthousiasme et confiance envers notre travail ! L'aventure se termine, d'autres sont à imaginer... Merci à tous !...  Actualité 
Expositions Nouveautés 2008  Les germoirs à graines Art du trait Le tracé du pentagone |
|