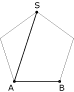
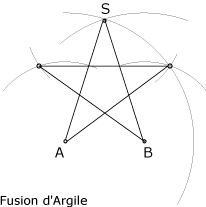
Dans un pentagone convexe régulier comme ci-dessous... :
...on a : AS / AB = phi
(le nombre d'or)
Comme nous savons tracer Phi à partir d'un segment donné (voir l'historique des articles en bas de page),
il nous est facile de tracer un pentagone régulier en connaissant
un des côtés.
Moins évident peut-être, est le tracé du pentagone à partir
du cercle circonscrit. Nous le présenterons ensuite.
Tracé du pentagone par un côté connu
Appelons AB, le côté connu (mesuré).
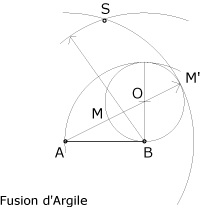
On reprend le tracé du nombre d'Or, ce qui nous donne comme on l'a vu :
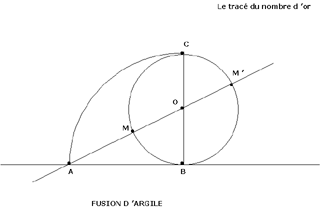
On sait que AM' = phi . AB
et donc le tracé du pentagone est très simple :
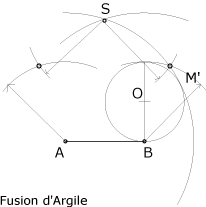
1. Tracer au compas un arc de cercle de rayon AM' à partir de A et à partir de B.
Ces arcs se coupent au sommet "opposé" (ici S) au côté AB du pentagone.
1. Ouvrir le compas sur A et B.
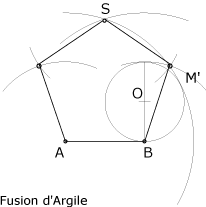
2. Tracer de A, de B puis de S, les arcs de cercle nécessaires pour positionner les deux autres sommets.
On trace un pentagone régulier en joignant les sommets successifs.
Si l'on joint les sommets deux à deux on obtient le pentagone concave (une étoile régulière)
Cette étoile était l'un des symboles "principaux" de Pythagore et de ses disciples...
Elle a également inspiré Léonard de Vinci...
et bien d'autres...
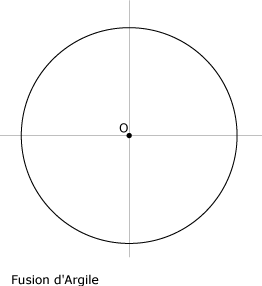
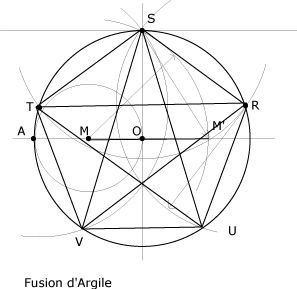
Tracé du pentagone avec le cercle circonscrit
Nous disposons donc d'un cercle, inscrivant le pentagone régulier :
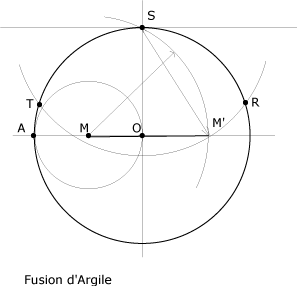
1. On marque le milieu du rayon OA (ici M)
2. Le compas ouvert de M à S, on trace l'arc redescendant sur le diamètre "horizontal" jusqu'à M').
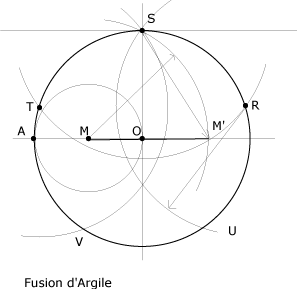
3. De S par M', on trace un arc interceptant le cercle en T et R.
1. On marque les points U et V.
1. On trace le polygone.
Bibliographie :
Matila C. Ghyka : nombreux ouvrages...
Historique des rubriques :
|