Triangle d' Or
Un Triangle d' Or est un triangle isoclèle tels que la proportion d'un côté par rapport à la base soit Phi,
le nombre d' Or.
Les Triangles isocèles dont c'est la base par rapport au côté qui soit Phi sont aussi appelés
Triangles d'Argent.
On construit aisément un Triangle d' Or à partir du Rectangle d' Or(voir "La Spirale d' Or" dans l'historique en bas de page) de la façon suivante :
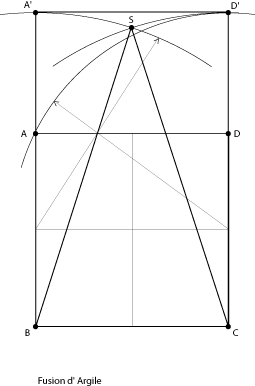
Spirale d' Or avec le Triangle d' Or
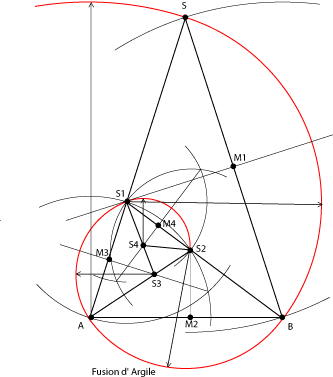
Nous disposons donc d'un Triangle d' Or
1. On trace la médiatrice de SB (milieu M1). Elle coupe SA en S1.
On trace S1B. Le triangle S1BS est un Triangle d' Argent, et le triangle BS1A est d'Or.
2. On poursuit de même avec la médiatrice de AB (milieu M2). Elle coupe S1B en S2.
3. On trace AS2. S2AB est un Triangle d' Argent. AS2S1 est un Triangle d' Or.
4. On continue selon le même principe pour tracer S3 et S4 (avec les médiatrices en M3 et M4).
Une méthode plus simple serait de tracer des arcs de cercle à partir du point 2 ci-dessus.
Ainsi
2. Au compas de A à S1, marquer S2 sur S1B.
3. Au compas de S1 à S2, marquer S3 sur AS2
4. Au compas de S2 à S3, marquer S4 sur S1S3, etc...
5. On trace les arcs S2S1 de centre S4, S1A de centre S3, AB de centre S2 BS de centre S1, et plus loin que S par
un arc de centre A ... pour tracer la Spirale.
Le Nautilus, étrange animal marin, est l'exemple emblématique de la spirale
dans la Nature.
La spirale est un symbole présent dans de très nombreuses civilisations et cultures
du monde entier. Les formes sont nombreuses et la Spirale d'Or n'en est qu'un exemple.
Autres informations :
.
Historique des rubriques :
| 








